MÓDULO 7: NOCIONES DE TRIGONOMETRÍA
Razones trigonométricas: Teorema de Pitágoras. Definición de cateto opuesto y de cateto adyacente. Uso de la calculadora. Problemas del observador: Ángulo de elevación y ángulo de depresión.
En la imagen se observa que para obtener la medida de la altura de la torre es necesario recurrir a conceptos de trigonometría, específicamente aquellos relacionados con la resolución de triángulos rectángulos. En general, en situaciones en las cuales por razones de inaccesibilidad no es posible medir un objeto directamente, se recurre a conceptos de trigonometría.
Recordemos que resolver triángulos significa calcular la medida de sus lados y la amplitud de sus ángulos y para tal objetivo los conceptos a aplicar son: teorema de Pitágoras y Razones trigonométricas.
Los ejemplos y casos que siguen tienen por objeto favorecer la comprensión de estos conceptos mediante distintos sistemas de representación que aluden a visualizaciones e interpretación de lenguaje matemático.
El teorema de Pitágoras relaciona la medida de los tres lados de un triángulo rectángulo. Si bien su enunciado es muy conocido (el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos), importa que se comprenda qué significado tiene esta relación, cuál es el porqué de la misma:
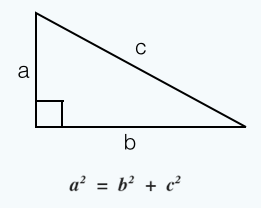
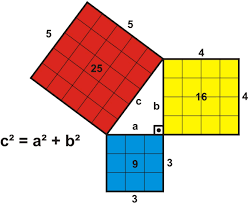
Para lo cual es fundamental que interpretando el lenguaje matemático empleado en la fórmula se “lea” que a2 (a elevado al cuadrado) es visualmente el área de un cuadrado de lado “a”, análogamente b2 representa el área un cuadrado de lado “b” y y “c2 ” el área de un cuadrado de lado c.
Luego, interpretando el teorema de Pitágoras, podemos decir que el área del cuadrado (con lado en la hipotenusa) es igual a la suma de las áreas de los cuadrados con lados en cada uno de los catetos.
Los siguientes ejemplos permiten visualizar esta situación a partir de una “demostración acuática” y de la resolución de un tangram.
Actividad interactiva
Ingresá a la siguiente actividad interactiva. El objetivo de esta actividad es que comprendas qué significado tienen las razones trigonométricas, como por ejemplo la expresión “cos (a) = Cateto adyacente /hipotenusa” (coseno del angulo “a”).
Esta actividad muestra que manteniendo fijo el ángulo y cambiando la medida de los lados del triángulo, en este caso el cateto adyacente al ángulo y la hipotenusa, su relación (cateto adyacente / hipotenusa) permanece constante. Luego el coseno de un ángulo es un número que muestra la relación entre el cateto adyacente y la hipotenusa, que siempre es la misma por más que se cambien sus medidas.
Por ejemplo:
Cos (a) = ½ significa que en un triángulo con un angulo fijo “a” , la medida del cateto adyacente es la mitad de la medida de la hipotenusa.
Jugamos con tecnología
Esta actividad persigue un doble objetivo. El primero es que conozcas herramientas tecnológicas incorporadas en tu celular, en este caso calculadora de triángulos rectángulos. El segundo objetivo es que uses el lenguaje matemático incorporado al trabajar con los conceptos abordados para entender cómo usar la aplicación y luego emplearla para resolver problemas relacionados.
Interpretá la información que aporta la imagen.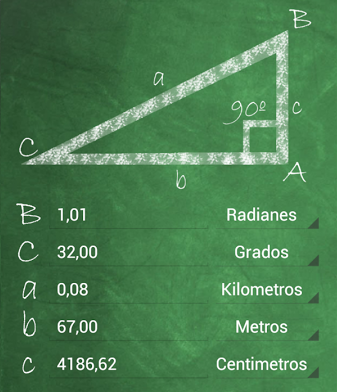
Actividad de cierre
Finalmente, te proponemos que realices la siguiente actividad de cierre. Su objeto es que autoevalúes tu aprendizaje resolviendo las actividades.
