ACTIVIDADES COMPLEMENTARIAS
Actividad 1
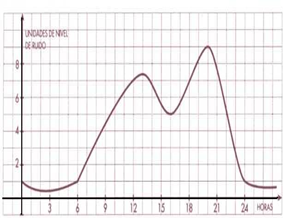
I. Un tanque cilíndrico vacío de 200 litros de capacidad se usa como depósito de agua. Una canilla ubicada en la parte superior comienza a bombear agua al depósito con una
rapidez constante de 10 litros por minuto.
a) ¿Cuál es la variable independiente? ¿Cuál es la variable dependiente?
b) A medida que el tiempo transcurre, ¿cómo cambia el nivel de agua en el depósito? Explicá.
c) Escribí un modelo matemático y luego realizá un gráfico que permita describir la relación existente entre el nivel del agua y el tiempo transcurrido.
d) ¿En cuánto tiempo la altura del agua estará a la mitad de la capacidad del tanque?
II. Analizá las preguntas anteriores considerando que inicialmente el tanque contiene 30 litros de agua.
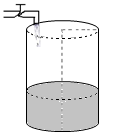
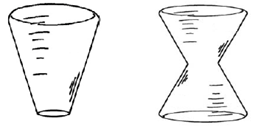
III. ¿Para cuál o cuáles de los siguientes recipientes el llenado se puede modelar con una función como la de los incisos anteriores? Explicá tu elección.
Actividad 2
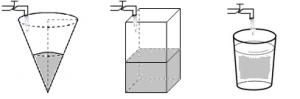
En una práctica de laboratorio se realizó el llenado de algunos recipientes con agua. Una llave controla el flujo del agua desde un depósito, por lo que siempre se tiene la misma cantidad de agua cayendo al recipiente. Teniendo en cuenta que los recipientes tienen base plana, realizá la gráfica de la altura en función del tiempo que modela el fenómeno en cada caso.
Actividad 3
I. Suponiendo que la rapidez de entrada de agua al depósito es de 6 litros por minuto y la de salida es de 4 litros por minuto.
a) ¿Cuál es la razón de cambio de la cantidad de agua en el depósito con respecto al tiempo?
b) Llamando V a la cantidad de agua en el depósito (en litros) y t al tiempo (en minutos), completa la siguiente tabla con los valores de V correspondientes a los valores de t dados.
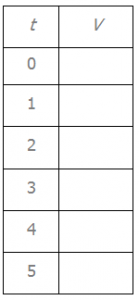
c) Expresá V en función de t.
d) Si el depósito tiene una capacidad para 40 litros. ¿Cuántos minutos deben transcurrir para que se llene?
e) Representá en un sistema de coordenadas cartesianas, la gráfica de V con respecto a t.
II. Suponiendo que la rapidez de entrada de agua al depósito es de 4 litros por minuto y la de salida es de 6 litros por minuto.
a) ¿Cuál es la razón de cambio de la cantidad de agua en el depósito con respecto al tiempo?
b) Llamando V a la cantidad de agua en el depósito (en litros) y t al tiempo (en minutos), completá la tabla con los valores de V correspondientes a los valores de t dados.

c) Expresá V en función de t.
d)¿Cuántos minutos deben transcurrir para que el depósito se vacíe por completo?
e) Representa en un sistema de coordenadas cartesianas, la gráfica de V con respecto a t.
Actividad 4
Considerá los tanques que se muestran en la figura.
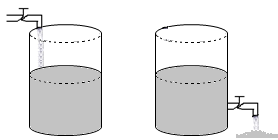
A través de las canillas abiertas, el agua entra al tanque A a razón constante de 4 litros por minuto y sale del tanque B a razón contante de 6 litros por minuto. Inicialmente, t = 0, el tanque A contiene 10 litros de agua mientras que el tanque B contiene 120 litros.
a) Determiná la expresión algebraica que expresa la cantidad de agua V en el tanque A en función del tiempo t.
b) Determiná la expresión algebraica que expresa la cantidad de agua V en el tanque B en función del tiempo t.
c) Encontrá cuántos minutos deben transcurrir para que los dos tanques contengan la misma cantidad de agua. Calculá cuántos litros de agua tienen los tanques en ese momento.
d) Si el tanque A tiene una capacidad para 150 litros. ¿Cuántos minutos deben trasncurrir para que se llene?
e) ¿En qué momento se vacía por completo el tanque B?
f) Representá en un mismo sistema de coordenadas cartesianas, la gráfica de V con respecto a t, para ambos tanques.


 En la imagen observamos un auto y una bicicleta que transitan por una calle. Ante esta situación podemos preguntarnos, por ejemplo, cómo varía la velocidad de cada uno a medida que transcurre el tiempo, qué distancia recorrerán en determinado intervalo de tiempo, cuánto tiempo debe transcurrir para que el auto pase a la bicicleta. En todas estas alternativas se relacionan distintas variables: distancia recorrida, velocidad, tiempo.
En la imagen observamos un auto y una bicicleta que transitan por una calle. Ante esta situación podemos preguntarnos, por ejemplo, cómo varía la velocidad de cada uno a medida que transcurre el tiempo, qué distancia recorrerán en determinado intervalo de tiempo, cuánto tiempo debe transcurrir para que el auto pase a la bicicleta. En todas estas alternativas se relacionan distintas variables: distancia recorrida, velocidad, tiempo.